Custom Phylogenetic Tree Construction Service
With state-of-the-art computing facilities and experienced professional science teams, Creative Biostructure provides custom phylogenetic tree construction service with various methods for protein evolution and genetic researches. We offer phylogenetic trees constructed with multiple methods for different applications, including unweighted pair group method with arithmetic mean (UPGMA), neighbor-joining (NJ), maximum parsimony (MP), maximum likelihood (ML) and Bayesian method.
Distance matrix methods: UPGMA and NJ
Both UPGMA and NJ are distance methods that need a distance matrix. The UPGMA is a hierarchical clustering or simple agglomerative method that based on the molecular clock hypothesis, which suggests a constant molecular evolution rate. This hypothesis must be tested and justified for the data set being applied before the UPGMA method is carried out for the construction of phylogenetic trees. UPGMA is often applied to establish guiding trees for more advanced phylogenetic algorithms. NJ method, however, is a bottom-up clustering method for the construction of phylogenetic trees. NJ method is applied for trees based on DNA or protein sequence data. Information of the distance between each pair of taxa is necessary for the algorithm to form the tree. The NJ algorithm starts with an entirely unresolved tree, and iterates its calculating steps until all the branch lengths are known and the tree is completely resolved.
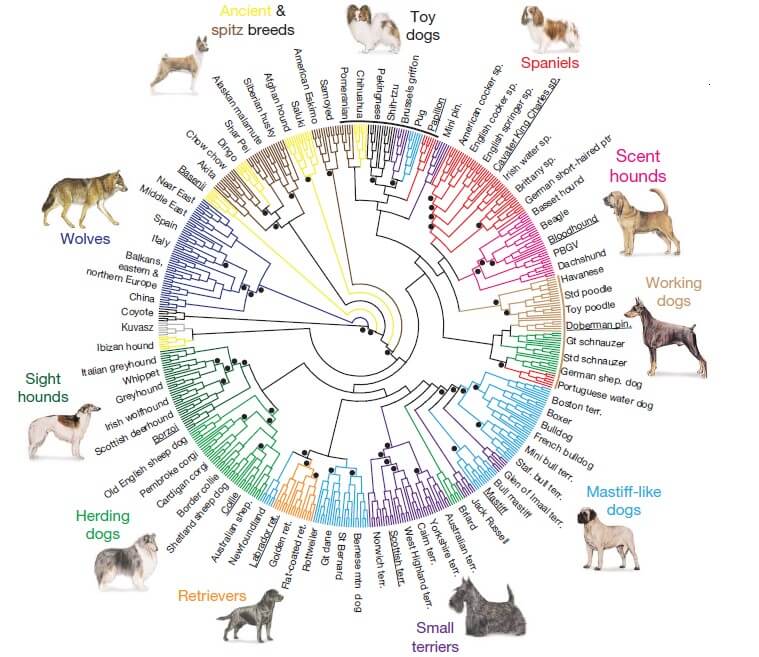
Figure 1. Neighbor-joining trees of domestic dogs and grey wolves
Discrete character methods: MP and ML
Discrete character methods determine the most likely ancestral relationships by the individual substitutions among the sequences. MP and ML are the most applied discrete character methods. The MP method predicts the phylogenetic trees that minimize the number of necessary steps to generate the observed variation in the sequences from common ancestral DNA or protein sequences. MP is applied with most kinds of phylogenetic data, and it was the only widely applied discrete character methods used for morphological data until recently. The ML method is a general statistical method for estimating unknown parameters of a probability model. It finds the value of one or several parameters for a given statistic which can make the known likelihood distribution a maximum value.
Bayesian method
Among all the methods, the Bayesian method is recognized as the most accurate methods. Bayesian inference is becoming popular in the field of phylogeny because of its integration of Markov chain Monte Carlo (MCMC) algorithms. The Bayesian method uses a likelihood function to create a quantity named the posterior probability of trees using an evolution model. It will construct the most likely phylogenetic tree for the given data set based on several prior probabilities. Bayesian method has been applied in many molecular phylogenetic and systematic researches.
Creative Biostructure helps you to construct the optimal phylogenetic tree with faster calculating speed and lower cost. The phylogenetic trees will be tested by our state-of-art analytic software. All the methods above are available in Creative Biostructure to meet different requirements.
With our service, your phylogenetic trees will be constructed more effectively with higher reliability and lower cost. Please feel free to contact us for a detailed quote.
Ordering Process
References
- Tamura, Koichiro, et al. "MEGA5: molecular evolutionary genetics analysis using maximum likelihood, evolutionary distance, and maximum parsimony methods." Molecular biology and evolution 28.10 (2011): 2731-2739.
- Huelsenbeck, John P., et al. "Bayesian inference of phylogeny and its impact on evolutionary biology." Science 294.5550 (2001): 2310-2314.
- Guindon, Stéphane, and Olivier Gascuel. "A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood." Systematic biology 52.5 (2003): 696-704.
- Lewis, Paul O. "A likelihood approach to estimating phylogeny from discrete morphological character data." Systematic biology 50.6 (2001): 913-925.

